みんな大好きプレゼント交換
―プレゼント交換。良い響きですね。子供のころ地域の集会や学校でやった記憶があります。大人になった今もやってみると意外と楽しいのが、このプレゼント交換。

単純な誕生日や記念日に送るプレゼントと違って、参加する人たちである程度予算を決めてその“予算内”で“誰が貰っても喜ぶ”ものを選ばなければいけないという難しさも楽しみにのひとつ。女混合になるとさらにこの難易度は増します。そういうときは大体女子寄りのプレゼントを買うといいという説が僕の中ではあります。笑
さて、このプレゼント交換で一番起きたらガッカリすることはなんでしょうか。
おそらく、「自分のプレゼントが自分のもとに返ってくる」という出来事ですね。もちろんそうなってしまったら、もう一度やり直したり部分的に交換したりといくつかの対処法はございます。
でも、そういう工夫を抜いて単純に“全員が自分のプレゼントを受け取らない”確率って実際どれくらいなのでしょうか。せっかくなのでちょっと考えてみましょう。
今回はそれについてご紹介していきます。

5人でプレゼント交換する時を例に考えて見ましょう
まずは、起きてはいけない事が何かを整理しておきますね。5人がプレゼント交換をするとします。そして、それぞれがプレゼントを用意したシチュエーションを想像して下さい。
A-a , B-b , C-c , D-d , E-e
大文字のAからEが人で、小文字のaからeがそれぞれが用意したプレゼントです。プレゼント交換をして、たとえば
A-e , B-c , C-b , D-a , E-d
というように、それぞれがバラバラになればOKとしましょう。逆に、
A-e , B-b , C-e , D-d , E-c
というように、一人でも自分のが手元に来てしまったらNGとします。(上でいうと、Bの人が自分のプレゼントbを受け取ってしまっています。Dさんもdを受け取ってますね)
この全員が自分のプレゼントを受け取らない確率については、以下のような一つの数式で表すことができます。
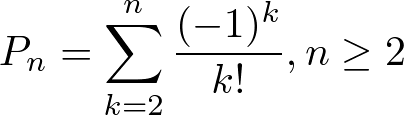
nはプレゼント交換する人数(=プレゼントの数)です。高校数学レベルの数式が出てきましたが、そこまで理解しようとしなくてOKです。「公式があるんだ~」程度で認識ください。この数式の導出方法などについてここに書いていくと非常に長くなってしまうので、もし気になる方は、
「モンモール数」や「完全順列」などのワードで探すと導出方法などが出てくると思いますの検索してみてください。
そして、この数式を使って計算していくと、
2人、3人、4人、5人、6人、で交換するとき誰か一人でも「自分のプレゼントが自分のもとに返ってくる」確率はそれぞれ、
2人→50%
3人→33.333…%
4人→37.5%
5人→36.666…%
6人→36.805…%
となります。2人の時は50%と高いですが、通常プレゼント交換は3人以上でやりますので、大体30%台で誰か一人には自分のもとに返ってくる事が分かります。面白い事に、どんなに人数が増えてもおおよそ36.788%の確率で自分が自分のプレゼントを受け取らずに済むのです!
(詳しく言うと、n→∞のとき確率は1/eに収束します)
おおよそ3回に1回、うまく交換できるというわけですね。言い換えると3回に2回はうまく交換することが出来ないわけです!意外と難しい!
うまく交換できない確率の方が大きい訳で、あらかじめうまくいかなかった時の対策を考えておいた方がよい、という事でしょう。そして、この確率は人数によって大きく左右されないということもポイントですね。
それではぜひ、楽しいプレゼント交換を!
(証明終了)